Similarity Search for Grouped Content (Teaser)
30 Apr 2023Vector search has taken the world by storm. The idea is this - cast documents into a vector embedding space via some transformation (e.g. BERT) and then index them into a vector database that is capable of fast approximate nearest neighbors search. Then when the user makes a text query, cast their query into this same embedding space and find the nearest vectors to the query vector and return the corresponding documents.
It occurred to me today while staring at the sky blankly, that this type of search won’t work when searching for grouped content. For instance, what if I go onto Reddit, and I’m not really looking for a single reddit page, but I’m looking for an entire subreddit that matches my interests. Here I’m not looking a document, but a group of documents that match my intent.
So how could we make this search work? Well the most obvious and naive way is that for every subreddit, we could concatennate all the entries into a single mega-document, and use our embedding transformation to make a single vector for every single subreddit. Not only would this be technically infeasible, it wouldn’t really be a great search experience either. Why? Because a subreddit is composed of many docs which form a cloud of points rather than a single point in the embedding space.
Gaussian Search
What if we preserved the cloud of content rather than reducing it to a point? Well first, why would it even be important to preserve the cloud of content? Consider figure A below. The red point represents a user’s query “female vocalists”, and the green points represent two different subreddits reduced to a point. Which subreddit is more relevant to the query? The answer is ambiguous by design – I’ve place the query equidistant from the two subreddits.
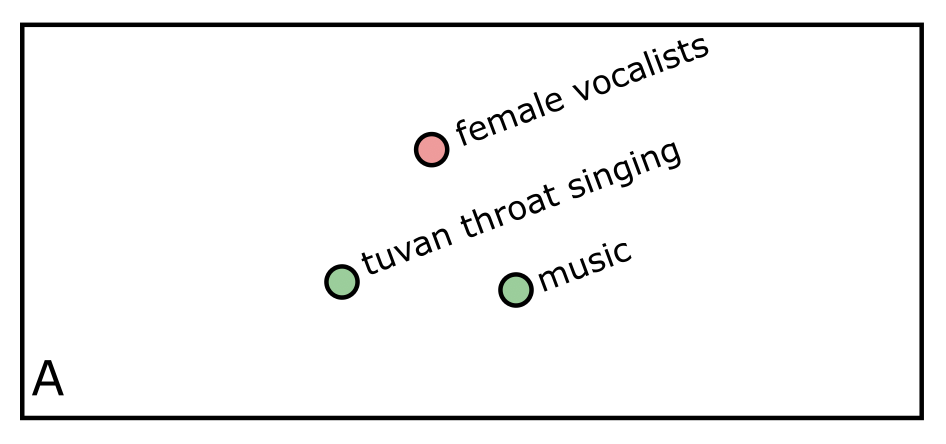
However, looking at figure B, if we preserve the cloud of documents within each subreddit, we see that the “tuvan throat singing” subreddit is considerably more focused than the “music” subreddit and the user’s query is at the edge of it’s content cloud. So when we preserve the cloud of content, the broader “music” subreddit is likely a better choice for this query.
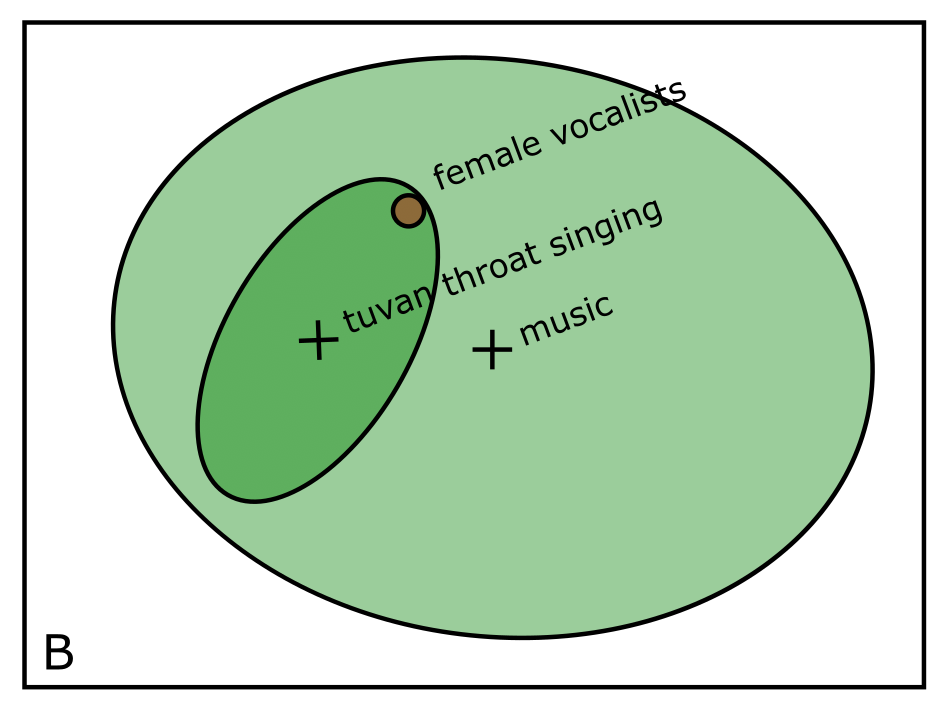
Notice that I’m calling this “Gaussian” search? The reason is that I’m proposing that each grouping of documents be modeled as a Gaussian distribution in embedding space. This will serve us well as Gaussians are really easy to specify using matrices. For instance, a Gaussian (or Normal) distribution is usually represented in 1-D as \(N(\mu, \sigma^2)\) where \(\mu\) is a scalar representing the mean of the distribution and \(\sigma^2\) is a scalar representing the variance. In higher dimensions this becomes \(N(\boldsymbol{\mu}, \boldsymbol{\Sigma})\) where \(\boldsymbol{\mu}\) again represents the mean, but this time it’s a vector and \(\boldsymbol{\Sigma}\) is again the variance but it’s a matrix. To sorta make this clearer, consider the equation:
\[M = (\boldsymbol{x} - \boldsymbol{\mu})^T\boldsymbol{\Sigma}^{-1}(\boldsymbol{x} - \boldsymbol{\mu})\]\(M\) is the Mahalanobis distance, and if you hold M constant, then the resulting locus of points \(\boldsymbol{x}\) form an ellipsoid just like those in the illustration above.
Simple? Intuitive? Well… no, not immediately, but the important thing to know is that there is a direct connection between the “space that a subreddit takes up” and a numerical representation defined by \(\boldsymbol{\mu}\) and \(\boldsymbol{\Sigma}\), and now that we’re in the land of numbers, then perhaps we can have computers answer questions about these numbers. In this case, the question is which group of content is “closest” to the users query in terms of Mahalanobis distance.
Gaussian-to-Gaussian Search
There’s a possible problem in the above formulation. In just the same way that the content group isn’t describable by a single point, the user’s query likely also covers a volume of the embedding space rather than just a point. Consider figure C below. Once we see how large of a domain “female vocalists” covers, then perhaps “tuvan throat singing” begins to look a little more relevant.
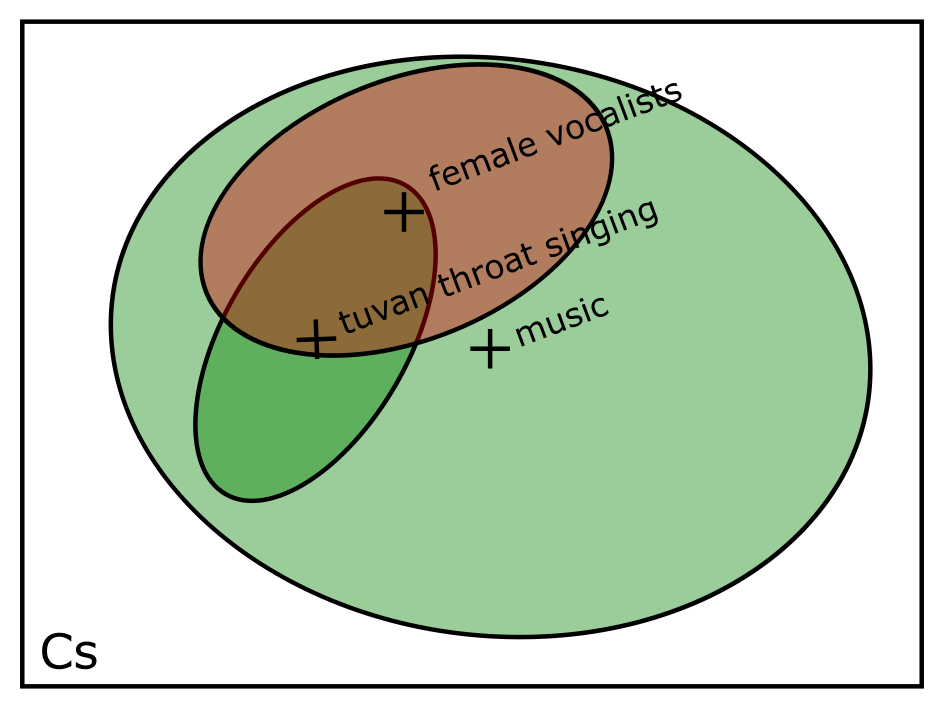
This implies that we would want a different way of measuring similarity. Rather than Mahalanobis distance, perhaps we can use something like Kullback–Leibler divergence to measure how similar the query is to each cluster.
Mixed Gaussian Search
The natural next point is that Guassians themselves are likely not a great model for content groups. But if we describe the content groups as a mixture of Gaussian distributions, then, by including enough Gaussian distributions, we’re guaranteed to have a good model for the content distribution.
What to Do Next
This is a mind-meld teaser post meaning that I wrote it just to get the idea out there. But if you are interested, you can work with me to help complete it. (Interested? Contact me: jfberrymanⓐgmail·com.)
I think the most interesting direction to take this research is to see if we can follow the intuition of Hierarchical Navigable Small Worlds (HNSW) and come up with a data structure to quickly find the closest clusters in terms of Mahalanobis distance. That’s plenty hard enough, but if we figure that out, then maybe we could tackle the harder problem of assuming the user’s query is also a Gaussian and figuring out some way to quickly determine overlap the the user’s query Gaussian with every content cluster Gaussian.